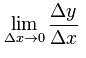Математика для фізиків

Поняття похідної

В кожній точці, похідна функції f(x) = 1 + x∙sinx² дорівнює нахилу лінії, яка дотична до кривої. Коли похідна додатня — дотична зелена, коли від'ємна — дотична червона, а коли дорівнює нулю — чорна.

 1. Означення  

Нехай в деякому околі точки x₀ визначена функція f. Якщо ми візьмемо довільне число x в цьому околі, то приріст аргументу (Δx) в цьому випадку визначається, як x−x₀, а приріст функції (Δy) — як f(x)−f(x₀). Тоді, якщо існує границя

то вона називається похідною функції f в точці x₀.

Або:   

похідна визначається як границя відношення приросту функції до приросту її аргументу коли приріст аргументу прямує до нуля (якщо така границя існує).

Функцію, що має скінченну похідну, називають диференційовною.

Процес знаходження похідної функції називається диференціюва́нням. 

Зворотним до диференціювання є інтегрування — процес знаходження первісної.

 2. Геометричний зміст похідної  

Геометричний зміст похідної: значення похідної функції y = f(x) у точці x₀ дорівнює кутовому коефіцієнту дотичної до графіка функції в точці з абсцисою x₀:

y' = f'(x₀) = k = tgα.

 3. Фізичний зміст похідної   

Похідна від фізичної величини вказує на швидкість її зміни:

• похідна координати за часом дорівнює миттєвій швидкості матеріальної точки;

 v = x'(t),

• похідна від швидкості за часом дорівнює швидкості зміни швидкості матеріальної точки, або її прискоренням;

  a = v'(t),

• похідна від заряду за часом дорівнює швидкості зміни заряду з часом або силі струму;

 I = q'(t)

• похідна від магнітного потоку з часом дорівнює швидкості зміни магнітного потоку або Е.Р.С. індукції, взятої з від’ємним знаком;

E = -Ф'(t)

• похідна від імпульсу матеріальної точки за часом дорівнює швидкості зміни її імпульсу або силі, яка спричиняє цю зміну;

F = p'(t) …

3. Похідні основних елементарних функцій

 Похідні від простих функцій

 Похідні від експоненціальних та 

логарифмічних функці

 Похідні від тригонометричних функцій

 4. Основні правила диференціювання  

 5. Застосування похідної для дослідження функцій  

Якщо y'(x) > 0, то функція зростає.
Якщо y'(x) < 0, то функція спадає.
Якщо y'(x) = 0 (або не існує), то в точці x = x₀ знаходиться екстремум функції (максимум або мінімум).

 6. Рівняння дотичної до графіка функції у = f(x) 

 y – y₀ = f '(x₀)∙(x – x₀)

де (х₀, у₀) – точка дотику.

Приклад:

Яка потужність виділяється на зовнішній ділянці кола (корисна)?

Р_к - ?

Р_к = ІU = U²/R = I²R = (E/(R +r))²∙R

При якому значенні R потужність, котра виділяється у зовнішній ділянці кола, буде максимальною?

(Р_R)' = 0

Р_R' = ((E/(R +r))²∙R)' = {(E²R)'∙(R + r)² - E²R∙(( R + r)²)'}/ (R + r)⁴ =0

E²( R + r)² = E²R∙2( R + r)

R + r = 2R

  r = 2R –R

 r = R